Landauer Limit
July 8, 2011
Our
computers dissipate a lot of
heat. The
CPU of some computers will dissipate more that a hundred
watts under peak conditions. According to
data supplied by Intel, the
Intel Pentium D Processor 960 has a peak power dissipation of 130 Watts. Does it really take that much power to do computation, or is all this heat just a reminder that we still don't know how to build efficient electronics?
That sounds like a problem for a
physicist to tackle. Computer pioneer and physicist,
John von Neumann, was the first to realize from
entropy considerations that there must be a finite
energy involved in computation, but it wasn't until 1961 that the problem was rigorously tackled by
Rolf Landauer of
IBM.[1] Landauer reasoned that when a
bit of information is
irreversibly transformed, as in erasure, or when two bits combine
logically to yield just a single bit from the two, some information is lost.
Since
information and entropy are connected, it's possible to calculate the energy involved in the transformation of a single bit under ideal circumstances. This energy,
EL, known as the
Landauer limit is given as
EL = kT(ln2)
where k is the
Boltzmann constant, T is the
absolute temperature at which the computation takes place, and ln2 is the
natural logarithm of two, or about 0.69315. At room temperature, 298.15
K, this calculates out to be just 0.0178
electron volt. For those whose minds aren't calibrated in eV, this is just 2.8519 x 10
-21 joule.
Although the formal derivation of this formula is more involved, it's easy to see its logical basis. The
Boltzmann entropy,
S is given as
S = k(lnΩ)
where Ω is the the number of ways you can arrange items in a
thermodynamic system. When talking about bits of information, there are just two states, thus the ln2 term. One of
Maxwell's thermodynamic equations that I discussed in a
previous article (Maxwell's Other Equations, April 6, 2011) relates a change in
system energy,
dU, to a change in entropy,
dU = TdS - PdV
Our computers are not usually subjected to a
volume change,
dV, so we can ignore the
PdV term, where P is the
pressure. Combining the equations gives us a reason to believe in the Landauer limit.
Since a watt is a joule/sec, we should be able to perform at least 10
20 bit operations a second for just a watt expenditure. Compare this to the 9.89 megawatts it takes for the
RIKEN K Computer to perform 8.2
petaflops; that is, 8.2 x 10
15 floating point operations per seconds, as described in a
previous article (Special K, June 23, 2011).
A floating point operation does take a few bit operations to perform, so to be generous, let's say that these 8.2 petaflops convert to 10
20 bit operations per second, so our computing efficiency is about 0.00001%. We're obviously computing under the wrong
paradigm!
One possible way to increase computational efficiency is to change our mindset from using
electrons as
current carriers to using electrons as
magnets. I mentioned logic operations using the older
magnetic bubble technology and the newer
spintronic devices in a
previous article (Spintronics, February 1, 2011).
Electrical engineers at the
University of California at Berkeley are doing just that in a study published in
Physical Review Letters.[2-3]
The
UC-Berkeley team, led by
Jeffrey Bokor, Professor of Electrical Engineering and
Computer Science and scientific director of the
Molecular Foundry at
Lawrence Berkeley National Laboratory, has created nanomagnetic logic structures that are near the Landauer limit. One caveat is that their computational speed, given by changes in driving magnetic fields, was slow. The slow speed is probably necessary since thermodynamics always requires equilibrium, or quasi-equilibrium, states.
The team built a
majority logic gate from nanomagnets. In a majority logic gate, the output is determined by a majority "vote" of the inputs. In the example shown in the figure, there are three inputs and one output. Magnetic contrast imaging in the
Advanced Light Source at Lawrence Berkeley National Laboratory shows nanomagnets with the north pole facing downwards as bright spots (also represented by the red bars), and nanomagnets with the north pole facing upwards as dark spots (represented by the blue bars). The output is the second bar from the right, and its state is determined by the surrounding bars (top, left and bottom).
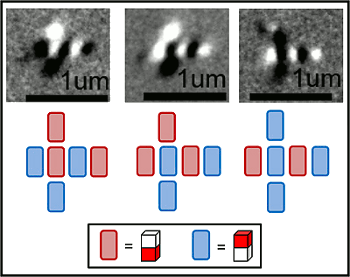
A majority logic gate formed from six nanomagnets.
The output reflects the majority vote of the three input.
See text for details.
(UC-Berkeley Image).
The nanomagnets used in this demonstration device were about 100 nanometers wide and about 200 nanometers long. The demonstration logic cell actually used electrical currents to generate the magnetic fields that flipped the magnetic bits. Said Brian Lambson, one of the coauthors of this work, "We are working now with collaborators to figure out a way to put that energy in without using a magnetic field, which is very hard to do efficiently... A multiferroic material, for example, may be able to control magnetism directly with a voltage rather than an external magnetic field."[3]
The work was supported by the
National Science Foundation.
References:
- Rolf Landauer, "Irreversibility and heat generation in the computing process," IBM Journal of Research and Development, vol. 5, no. 3 (July 1961), pp. 183-191. A PDF image can be found here.
- Brian Lambson, David Carlton, and Jeffrey Bokor, "Exploring the Thermodynamic Limits of Computation in Integrated Systems: Magnetic Memory, Nanomagnetic Logic, and the Landauer Limit," Physical Review Letters, vol. 107, no. 1 (July 1, 2011), Document No. 010604.
- Robert Sanders, "Magnetic memory and logic could achieve ultimate energy efficiency," University of California - Berkeley Press Release, July 1, 2011.
- Rolf Landauer, "Dissipation in Computation," Physical Review Letters, vol. 53, no. 12 (September 17, 1984), p. 1205.
Permanent Link to this article
Linked Keywords: Computer; heat; central processing unit; CPU; watt; Intel Pentium D Processor 960; physicist; John von Neumann; entropy; energy; Rolf Landauer; IBM; bit; irreversible process; logic gate; information; Landauer limit; Boltzmann constant; absolute temperature; natural logarithm; Kelvin; K; electron volt; joule; Boltzmann entropy; thermodynamic system; Maxwell's thermodynamic equations; system energy; volume; pressure; RIKEN K Computer; petaflops; paradigm; electron; current carrier; electron magnetic dipole moment; magnet; magnetic bubble technology; spintronic; electrical engineer; University of California at Berkeley; Physical Review Letters; Jeffrey Bokor; Computer Science; Molecular Foundry; Lawrence Berkeley National Laboratory; majority function; majority logic gate; Advanced Light Source; National Science Foundation.