
Conway Numbers
October 10, 2012 Numbers have so many properties that's it's easy to define numerous[1] sequences of integers. That's why the On-Line Encyclopedia of Integer Sequences™ now has more than 210,000 cataloged sequences. I wrote about the generator of many such sequences, The Collatz conjecture, in a previous article (The Collatz Conjecture, April 14, 2011) Here's the procedure for generation of Collatz integer sequences:1) Start with a natural number, n0Note the conditional statement expressed in steps 2-3. The conjecture, as expressed in step 4, is that such sequences will always terminate in one, independently of the starting value, n0. The conjecture is unproven, but all sequences tested have ended in one.[2] The following plot shows the sequence starting at n = 983.
2) If n is even, then ni+1 = ni/2
3) If n is odd, then ni+1 = 3ni + 1
4) Continue at step (2) until n = 1
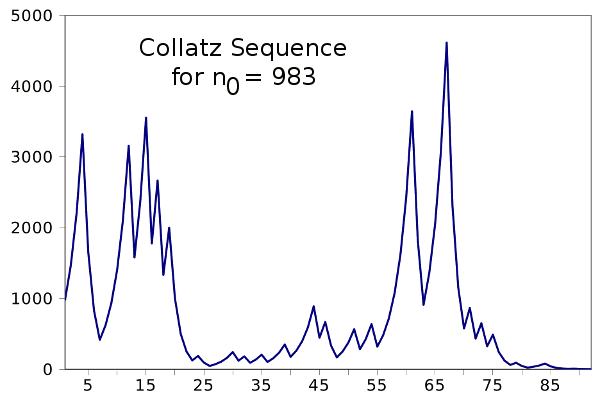 Collatz sequence starting with n = 983. This interesting recursion was discovered in 1932 by Lothar Collatz, who was at the time a twenty year old mathematics student. (Plot via Gnumeric)
As recalled in reference 3, when mathematician John Conway once visited Richard K. Guy, he spent some time in transit calculating subprime Fibonacci sequences, or Conway sequences as named in his honor. These sequences are built like the Fibonacci sequence, with two starting numbers. As in the Fibonacci sequence, the last two terms are summed to get the next term.[3]
The next term of a Conway sequence is not used as calculated, but it's also subject to a conditional statement, just as in a Collatz sequence. If the term is a composite number, you divide by its smallest prime factor to get the next term. Because of the conditional statement, these sequences exhibit pseudo-random behavior, and the sequence repeats after a number of cycles. You can see a schematic of the 56-cycle sequence in the figure.[3]
Collatz sequence starting with n = 983. This interesting recursion was discovered in 1932 by Lothar Collatz, who was at the time a twenty year old mathematics student. (Plot via Gnumeric)
As recalled in reference 3, when mathematician John Conway once visited Richard K. Guy, he spent some time in transit calculating subprime Fibonacci sequences, or Conway sequences as named in his honor. These sequences are built like the Fibonacci sequence, with two starting numbers. As in the Fibonacci sequence, the last two terms are summed to get the next term.[3]
The next term of a Conway sequence is not used as calculated, but it's also subject to a conditional statement, just as in a Collatz sequence. If the term is a composite number, you divide by its smallest prime factor to get the next term. Because of the conditional statement, these sequences exhibit pseudo-random behavior, and the sequence repeats after a number of cycles. You can see a schematic of the 56-cycle sequence in the figure.[3]
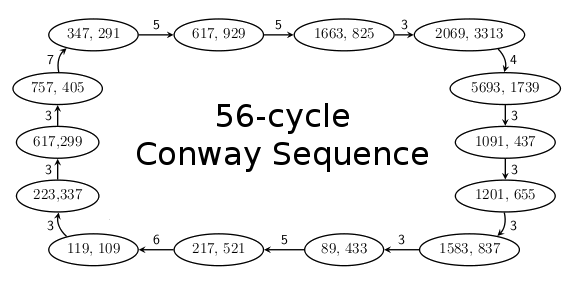 |
| The 56-cycle Conway sequence, from Richard K. Guy, Tanya Khovanova and Julian Salazar, "Conway's subprime Fibonacci sequences."[3] Shown are the nodes of the sequence, which are coprime odd integers not preceded by an odd term, and the number of terms between them. (Via arXiv Preprint Server)[3]. |
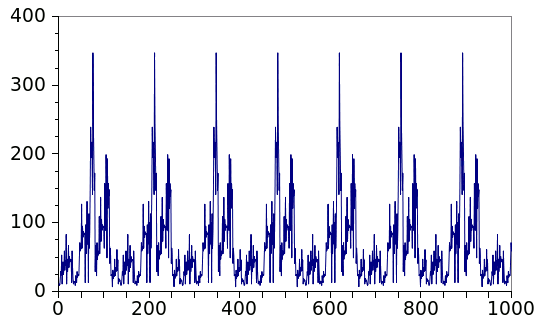 |
| The 136-cycle Conway sequence. Unlike the Collatz sequences, which terminate in one, this sequence is periodic after a few initial terms. (Graph rendered by Gnumeric). |
• A214892 - Conway's subprime Fibonacci sequence starting with (4,1)
• A214893 - Conway's subprime Fibonacci sequence starting with (18, 5)
• A214894 - Conway's subprime Fibonacci sequence starting with (10, 18)
• A214895 - Conway's subprime Fibonacci sequence starting with (23, 162)
• A214896 - Conway's subprime Fibonacci sequence starting with (382, 127)
• A214898 - Conway's subprime Fibonacci sequence, largest loop elements
• A214897 - Conway's subprime Fibonacci sequence : cycle lengths
Need I mention that Conway is best known for The Game of Life, which was a popular pastime when it was introduced in 1970?[4] The principal reason for its popularity is that it could be visualized on the primitive graphical environments of the time.
References:
- Pun intended.
- Jeffrey C. Lagarias, "The 3x + 1 problem and its generalizations," American Mathematical Monthly, vol. 92, no. 1, (January, 1985), pp. 3–23.
- Richard K. Guy, Tanya Khovanova, Julian Salazar, "Conway's subprime Fibonacci sequences," arXiv Preprint Server, July 21, 2012.
- Martin Gardner, "Mathematical Games - The fantastic combinations of John Conway's new solitaire game 'life'," Scientific American, vol. 223 (October 1970), pp. 120-123
- Richard K. Guy, Tanya Khovanova, Julian Salazar, "Conway's subprime Fibonacci sequences," arXiv Preprint Server, July 21, 2012.