
Rounded Corners and Squircles
October 13, 2011 When I was still doing experiments that required specialized hardware, I would enlist the services of our able machinists in their fully equipped machine shop. I would proudly show them my skillfully crafted CAD drawings, at which they were too polite to laugh, and they would ask me questions about the many details that I had left out. One question they would often ask is whether they should chamfer the edges. A chamfer is a beveled or rounded edge. The expression, "Nature abhors a vacuum," may be the paramount universal principle, but "Nature doesn't like hard edges or sharp corners," may be a close second. My son, unlike his amateur programming father, is an actual computer professional. He pointed out an interesting Steve Jobs story in his blog. Steve was a firm believer in the no-sharp-corners principle.[1] Bill Atkinson programmed QuickDraw, which was part of the Macintosh graphical user interface. The Motorola 68000 processor in the Macintosh was, as all microprocessors of the era, quite slow. There were, of course, no hardware floating-point operations, and integer multiplication and divisions were slow. Bill had devised a way to draw ovals that eschewed all the fancy math and used just additions and subtractions. As explained in Ref. 1, Bill used the fact that the sum of a sequence of odd numbers starting at one always equals a square; for example, 1 + 3 + 5 + 9 + 11 = 36. In general,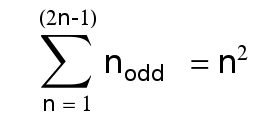 Steve, who was known to be a demanding character, was not that impressed. What Steve wanted was rectangles with rounded corners, and he quickly pointed out many examples in their office and outside environments. Bill went back to his development station, and in just a few hours he devised an algorithm that drew rectangles with rounded corners that was almost as fast as his ovals algorithm.
Steve, who was known to be a demanding character, was not that impressed. What Steve wanted was rectangles with rounded corners, and he quickly pointed out many examples in their office and outside environments. Bill went back to his development station, and in just a few hours he devised an algorithm that drew rectangles with rounded corners that was almost as fast as his ovals algorithm.
 | Steve Jobs and Bill Gates at 'D5: All Things Digital' conference in Carlsbad, California, 2007. (Photo by Joi Ito, via Wikimedia Commons). |
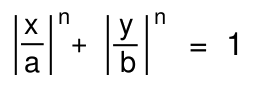 This equation generates a wide variety of closed curves, including the ordinary ellipse for n = 2. The ellipse, of course, becomes a circle when a = b. Other parameters will generate shapes that closely approximate a rectangle with rounded corners. For example, for a unit squircle, the parameters a and b are one, and the degree of "squareness" is set by the exponent, n. Large values of n give you shapes that look more like a square.
This equation generates a wide variety of closed curves, including the ordinary ellipse for n = 2. The ellipse, of course, becomes a circle when a = b. Other parameters will generate shapes that closely approximate a rectangle with rounded corners. For example, for a unit squircle, the parameters a and b are one, and the degree of "squareness" is set by the exponent, n. Large values of n give you shapes that look more like a square.
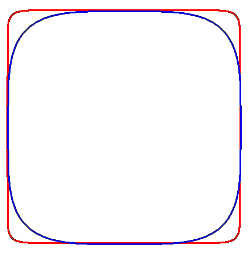 | Squircles for n=4 (blue) and n=16 (red) |
xi = 0.0625xi-2 + 0.0125xi-1 + 0.625xi + 0.125xi+1 + 0.0625xi+2and the corner was passed through this filter five time. More rounding can be achieved with a larger number of passes through the filter. The actual effect will depend on the granularity of the input data points. This process is most likely not original with me, but how would I know? I'm just a computer amateur.
yi = 0.0625yi-2 + 0.0125yi-1 + 0.625yi + 0.125yi+1 + 0.0625yi+2
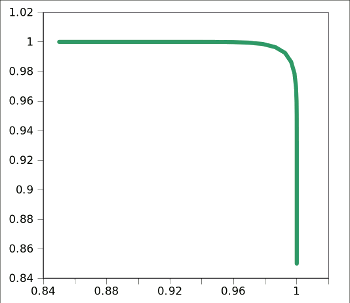 | Rounded corner obtained by passing a rectangle's data points through a low pass filter. Graph via Gnumeric using data from a C program by the author. (C program source code). |