
MEMS Resonator Logic Gate
April 4, 2011 Touch tone dialing has been with us since November 18, 1963, when pushbutton telephones were introduced in the US.[1] I must confess that since the standard pulse dialing was free, but tone dialing was offered as an additional monthly charge, my household stuck with pulse until recently. Modern telephone handsets with push buttons can convert key presses to pulses, so there was nothing lost there. We actually had a rotary dial telephone in our kitchen through 2009. The technology behind tone dialing is DTMF, dual-tone multi-frequency, signaling. It's an easy way to send simple digital messages down an audio line. You essentially choose two different frequencies and transmit this pair. Each of these two frequencies is chosen from its own palette of four frequencies, so you can get sixteen different codes. The first tone is chosen from 697, 770, 852 and 941 Hz; and the second tone is chosen from 1209, 1336, 1477 and 1633 Hz.[1] Tone generation, of course, is very easy; but you need eight upstream filters to decode the tones. It was likely the cost of these eight filters and associated logic that necessitated that extra monthly charge. Electronics in the 1960s was not cheap. Today, a single inexpensive chip can decode DTMF signals for multiple channels. Such tone decoding was taken to an extreme many decades later to increase the capacity of fiberoptic transmission lines. Instead of carrying data on just one frequency, wavelength-division multiplexing (WDM) puts data streams on many different frequencies, sometimes more than a thousand, all on the same fiber. An interesting paper in a recent issue of Nature Communications reports on research that utilizes resonance of a MEMS electromechanical resonator as a unique way to store and process digital signals. Such resonators store data bit as frequencies, and they can further perform logic tasks using these frequencies to perform the binary AND, OR and XOR functions. The research team was from the NTT Basic Research Laboratories, Kanagawa, Japan.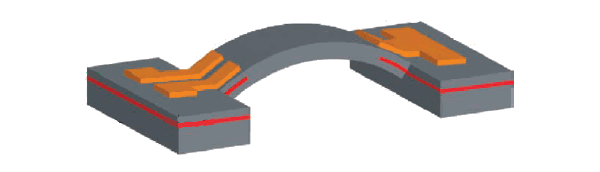 Depiction of the MEMS resonator (simplified from original), showing the overall geometry. Image licensed by the authors under the Creative Commons Attribution - NonCommercial - Share Alike 3.0 Unported License.
Their model resonator, as shown in the figure, was fabricated from a piezoelectric GaAs/AlGaAs heterojunction. The resonator beam is clamped at both ends, and it has dimensions 260, 84, and 1.35 μm. The oscillation mode is out of plane. The fundamental resonant frequency was 155,702 Hz, and the quality factor, Q = 140,000, puts it into the same class as a good quartz crystal. Unfortunately for potential applications of this approach, the resonator was held at a temperature of 3 K.
As a simple example of the resonator operation, we can represent two binary inputs, as follows:
Depiction of the MEMS resonator (simplified from original), showing the overall geometry. Image licensed by the authors under the Creative Commons Attribution - NonCommercial - Share Alike 3.0 Unported License.
Their model resonator, as shown in the figure, was fabricated from a piezoelectric GaAs/AlGaAs heterojunction. The resonator beam is clamped at both ends, and it has dimensions 260, 84, and 1.35 μm. The oscillation mode is out of plane. The fundamental resonant frequency was 155,702 Hz, and the quality factor, Q = 140,000, puts it into the same class as a good quartz crystal. Unfortunately for potential applications of this approach, the resonator was held at a temperature of 3 K.
As a simple example of the resonator operation, we can represent two binary inputs, as follows:
A: fA = 2 f0 + Δwhere fA and fB are frequencies corresponding to A and B that are applied to the resonator, f0 is the resonant frequency of the beam, and Δ is a fixed detuning frequency. The beam will resonant when excited by the second harmonic signal, 2 f0, but not when it's detuned. Thus, the presence of A or B alone will not excite resonance, but a combination of A and B will. In this case, the device acts as an AND gate. One interesting thing that the authors point out is that computers began as mechanical devices, and now computing has dipped back into its mechanical roots.
B: fB = 2 f0 - Δ
 | An example of mechanical computing. A portion of Charles Babbage's difference engine. Source: Harper's new monthly magazine, vol. 30, no. 175 (December 1864), p.34. (Via Wikimedia Commons) |