Tikalon Blog by Dev Gualtieri

A Foucault Gyroscope

February 14, 2011

One of the books on my bookshelf (a dead tree book, already twenty years old, and probably destined to last much longer than any electronic book) is Umberto Eco's , "Foucault's Pendulum ."[1] Eco is known also for The Name of the Rose , which became an excellent film starring Sean Connery [2] that few have seen. Eco is a professional semiotician , which is a perfect starting point for writing fiction.

I learned about Eco's Foucault's Pendulum while listening to National Public Radio (now known as NPR) on a drive back from the airport late one night after a business trip. The name of the book was easy for me to remember, since Foucault's Pendulum is an historic artifact that demonstrated the rotation of the Earth . The book is an unusual and entertaining mixture of topics, including vanity publication services , conspiracy theories , coded messages hidden in manuscripts , alchemy and ectoplasmic entities. The book takes its title from a scene in the Musée des Arts et Métiers which contained a pendulum with Foucault's original pendulum bob.[3]

In 1851, Foucault first demonstrated his pendulum at the Paris Observatory , but not after doing a proof of concept in his basement. His basement experiments were done at night, since daytime traffic added too much noise to his small, demonstration system.[4] The pendulum at the Paris Observatory had a ten meter wire, and it worked as expected. It was his massive 28 kilogram bob suspended on a 67 meter wire suspended from the from the dome of the Paris Panthéon that captured the most attention. The plane of swing of the pendulum rotated clockwise eleven degrees per hour; that is, it made a full circle in 32.7 hours. This was the calculated response for a pendulum at the latitude of Paris (48^o 48' N).

The reason the pendulum behaves this way is that the Earth rotates, but the pendulum maintains its motion with respect to absolute space ; or, as they said more poetically in Foucault's time, with respect to the fixed stars. Putting on our technologist cap, we see that if we carry such a pendulum with us, we'll always know our orientation with respect to a reference point. Better yet, if we could somehow have three orthogonal versions of the pendulum, we would know our precise three dimensional orientation.

Well, pendulums on a Foucault scale are too large to carry with us, and they only swing under the influence of Earth's gravity ; so, no orthogonal pendulums for you. However, Foucault's initial experiment wasn't with a pendulum. It was with a vibrating rod. He clamped the rod in the chuck of a lathe , struck it to get it vibrating, and then rotated the lathe.[4] Quite surprisingly, the rod continued to vibrate in its original plane. Such a vibrating rod will work as a direction sensing device, although with not much accuracy.

That's why gyroscopes were used for navigation before GPS, and even now in systems that can't rely on the presence of GPS , such as spacecraft . The mechanical gyroscope is well known to children, since it's a popular toy. Once it's set spinning, it will maintain its absolute orientation in space until the wheel runs down. A large gyroscopic mass spinning at high speed will give an accurate direction-sensing device. Navigation gyroscopes will use magnetic or other forces to keep the wheel rotating, although there's sometimes a sphere instead of a wheel.[5]

Engineers dislike mechanical systems, since they're usually less reliable than purely electronic systems; so, the ring laser gyroscope and its cousin, the fiberoptic gyroscope , were invented. These work on the principle, known as the Sagnac effect , that counter-propagating light beams around a closed path will shift in phase under rotation. The closed path is typically a rectangle or a triangle with a mirror at each apex. Unfortunately for the purists, a mechanical component is required in the most accurate RLGs, since the counter-propagating light beams will "lock" at rotation rates near zero and cause errors. This locking is usually defeated by having one of the mirrors vibrate.

MEMs systems , although mechanical, are generally more reliable than large mechanical systems. As a consequence, there are many types of MEMs gyroscopes . One caveat is that the most common MEMs gyroscopes don't monitor direction directly. They're accelerometers that measure the rate of change of angle. Electronic circuitry integrate this derivative signal to provide an absolute angle. As can be imagined, a lot of errors can creep into such an indirect system, but these sensors are useful in many applications for which long-term precision is not required.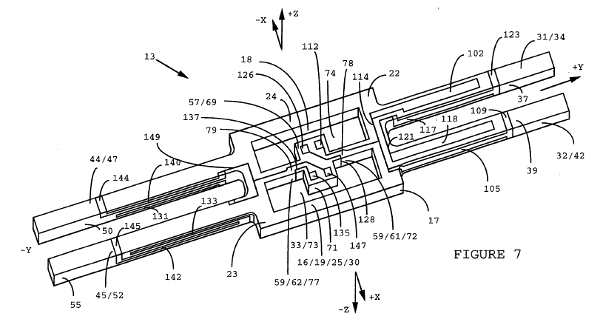

A tuning fork gyroscope. Fig. 7 of US Patent No. 5,396,144 (Piyush K. Gupta and Craig E. Jenson, "Rotation rate sensor with center mounted tuning fork," Mar 7, 1995; see Ref. 6.)

Most such MEMs gyroscopes are variants of a tuning fork . When a tuning fork rotates, the Coriolis forces on the vibrating tines will cause a torsional force at the base of the tuning fork that's easy to detect. The force is proportional to the angular rate. An example of an early implementation is shown in the above figure.[6] As you can see, turning a tuning fork into a useful angular rate sensor is somewhat difficult.

What would be especially desirable is a device that gives an orientation angle directly - A Foucault pendulum on a chip. Andrei M. Shkel , professor of mechanical and aerospace engineering at the University of California (Irvine), patented a Foucault concept in a MEMs device in 2002.[7] Shkel and his associates at the UC Irvine MicroSystems Laboratory have been improving this concept. The basic principle of such a gyroscope is shown in the figure below from Shkel's 2002 patent.[7]

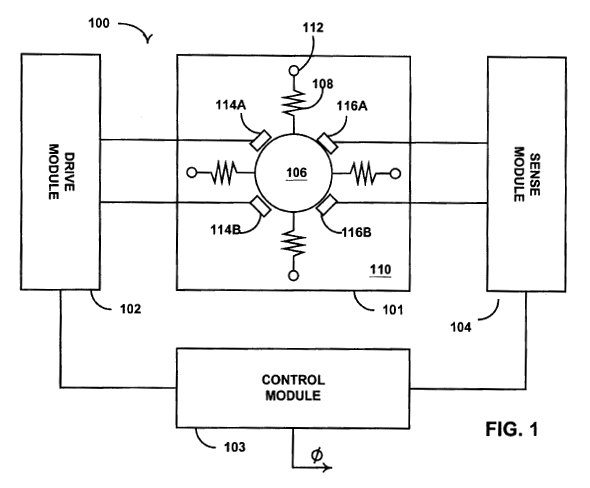A MEMs gyroscope inspired by the Foucault pendulum. Fig. 1 of US Patent No. 6,481,285 (Andrei M. Shkel and Roger T. Howe, "Micro-machined angle-measuring gyroscope," November 19, 2002; see Ref. 7.)

With reference to the figure, a large central mass (106) is held in place by springs or flextures (108) so that it's free to move in any direction in a plane. The suspension is isotropic ; that is, it has uniform stiffness in all directions in the gyroscope's plane, just as in a Foucault pendulum. Once the mass is driven to vibrate in a direction, it will continue to vibrate in that direction, even when the chip is rotated. The various sensors and actuators determine the direction of motion and apply a small driving force to keep the mass oscillating.

It all seems so simple; but, as usual, the devil is in the details , and it's difficult to fabricate such a device. Shkel, along with Igor P. Prikhodko, Sergei A. Zotov and Alexander A. Trusov of the UC Irvine MicroSystems Laboratory have presented a different Foucault pendulum architecture at The 24th International Conference on Micro Electro Mechanical Systems (MEMS 2011), Cancun, Mexico.[8-11] As shown in the figure, the design has not one, but four proof masses. this quadrupole version of a Foucault pendulum consists of four symmetrically vibrating tines that are synchronized by anti-phase levers .

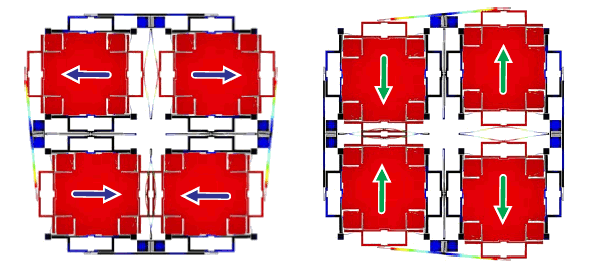Igor P. Prikhodko, Sergei A. Zotov, Alexander A. Trusov, and Andrei M. Shkel, "Foucault Pendulum On A Chip: Angle Measuring Silicon Mems Gyroscope," MEMS 2011, Cancun, MEXICO, January 23-27, 2011 (To be published).

Because of the symmetry, the vibrational modes in the "X" and "Y" directions are degenerate; that is, they occur at the same frequency. The rotation angle is given by the simple equation,

Θ = arctan(||y||/||x||)

where x and y are the displacement components. Experimental characterization of this device confirmed linearity in excess of ±450°/sec.

Acknowledgement:

Thanks to Dr. Alexander A. Trusov , Project Scientist at the UC Irvine MicroSystems Laboratory , for supplying information on the MEMs quadrapole Foucault Pendulum.

A Foucault Gyroscope

Acknowledgement:

References: